Esistono dei numeri magici in matematica, dove la loro combinazione è connessa alla geometria, alla fisiologia e all’anatomia. Questo magico accoppiamento può dar luogo a innumerevoli applicazioni e ispirazioni.
Alcuni di questi numeri non possono essere espressi sotto forma di frazione, ma possono essere definiti tramite dei radicali derivanti da particolari equazioni, questi numeri vengono detti irrazionali. Esempio la diagonale del quadrato di lato 1, identificata tramite l’equazione x2 = 2. Altro esempio di numero irrazionale, è il numero aureo 1,618…. che può essere ricavato dall’equazione polinomiale a coefficiente interi x2-x-1=0
Altri numeri, oltre ad essere irrazionali hanno la particolarità di essere anche trascendenti non essendo soluzione di equazioni, come ad esempio il PiGreco. I numeri irrazionali e quelli trascendenti sono dei numeri decimali infiniti.
Esiste anche una particolare successione di numeri, contenente questi numeri magici, detta successione di Fibonacci. Tale successione è rappresentata dalla seguente sequenza
Cioè ottenuta sommando ciascun termine con quello precedente. Questa particolare successione di numeri, vista così potrebbe essere poco apprezzata o meglio apprezzata solo dal punto di vista del calcolo ma sicuramente non stimola l’ intelletto del lettore. Scopriremo, invece, che questa sequenza nasconde un’infinità di applicazioni. Perciò, a scuola, bisogna far capire ai propri alunni che la matematica non è solo l’arte di saper fare i calcoli o di trovare la x in una determinata equazione. Oggi, in occasione del Fibonacci Day, scopriremo alcuni dei segreti nascosti in questa bellissima successione.
Leonardo Pisano, detto il Fibonacci, era figlio di Bo-naccio un impiegato doganiere a servizio dei commercianti pisani ad Algeri. Nel 1202 pubblicò un trattato “liber abaci”, ossia il libro dell’abaco che trattava la discussione di metodi e problemi algebrici mediante l’uso del sistema numerico decimale indo-arabico; dove per spiegare problemi usava sistemi frazionari a numeratore unitario, ponendo la parte e le parti frazionarie di un numero misto davanti alla parte intera. Ad esempio invece di scrivere 11 x usava scrivere la frazione a numeratore unitario x 11. Molto probabilmente questo sistema per Fibonacci doveva servire per facilitare i conti ai commercianti medievali. Ma l’importanza di questo libro non era per i metodi algebrici quanto nel trattare i problemi connettendo l’aritmetica con la geometria.
Il problema dei conigli
“Quidam posuit unum par cuniculorum in quodam loco, qui erat undique pariete circundatus, ut sciret quot ex eo paria germinarentur in uno anno, cum natura eorum sit per singulum mensem aliud par germinare et in secundo mense ab eorum nativitate germinant”.
Traduzione: Un tale mise una coppia di conigli in un luogo chiuso per sapere quante coppie sarebbero nate in un anno da quella coppia sapendo che in ogni mese da una coppia nasce un’altra coppia e che ogni coppia inizia a riprodursi nel secondo mese di vita.
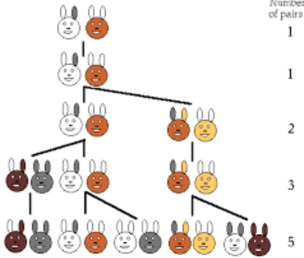
Ossia ciascun termine è dato (dopo i primi due) dalla somma dei due termini precedenti e che ci porta alla soluzione di 377 coppie al dodicesimo mese.
Tale serie possiede proprietà eleganti e significative. Ad ed esempio si può dimostrare che due termini qualsiasi successivi sono primi tra di loro.
Oppure, elevando al quadrato ogni numero e sommato con i successivi la scomposizione del numero ottenuto è sempre un numero di Fibonacci.
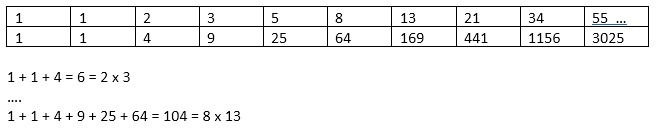
Altre applicazioni: Il rapporto tra il termine precedente e il suo successivo è il rapporto Aureo 1,618
Inoltre, con i quadrati possiamo costruire un rettangolo aureo
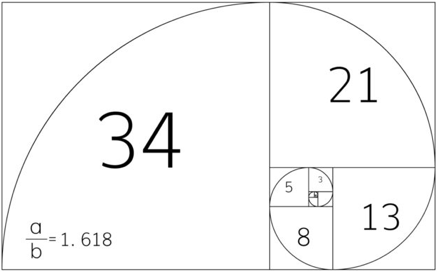
In ambito di applicazioni, questi numeri compaiono in natura, sorprendentemente i numeri dei petali di un fiore, oppure il numero di spirali di un girasole, o di un ananas, Nautilus, DNA, galassie e sulla Mole Antonelliana di Torino ecc.
Giuseppe Fiamingo
